Se sei pronto a salire di livello risolvi questa equazione quadratica e passa al livello successivo della sfida matematica.

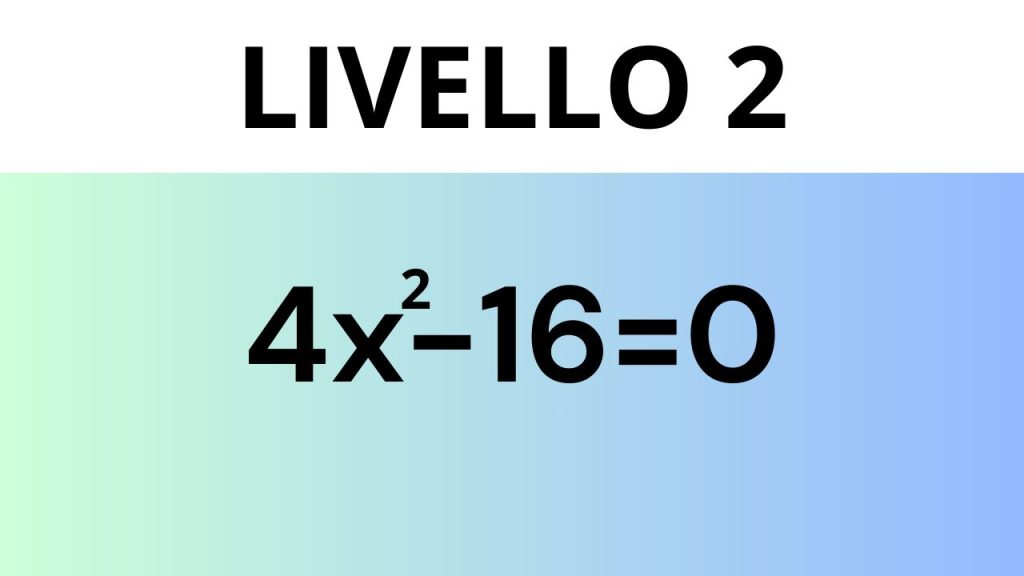
Benvenuti al Secondo Livello!

Dopo aver affrontato e superato l’equazione lineare del primo livello, è tempo di esplorare un terreno un po’ più complesso: le equazioni quadratiche. Queste equazioni sono fondamentali in molte aree della matematica e delle scienze applicate, e saperle maneggiare apre la porta a una comprensione più profonda di fenomeni naturali e tecnologici. Risolvi l’equazione e passa al terzo livello.

Equazione del Livello 2

Ecco l’equazione quadratica che dovrai risolvere:

4𝑥²−16=0

Perché Sono Importanti le Equazioni Quadratiche?

• Modellano fenomeni naturali, come la traiettoria di proiettili o la forma di ponti e archi.
• Sono essenziali in ottica, per descrivere lenti e specchi.
• Aiutano nella risoluzione di problemi di ottimizzazione, dove è necessario trovare massimi e minimi.

Guida alla Soluzione Passo per Passo

1. Porta tutti i termini su un lato:

Inizia organizzando l’equazione in modo standard:

4𝑥²=16

2. Dividi per 4:

Per semplificare, dividiamo ogni termine per 4:

𝑥²=4

3. Estrai la radice quadrata:

Per trovare 𝑥x, prendiamo la radice quadrata di entrambi i lati:

𝑥=±√4

4. Risultati:

Questo ci dà due soluzioni:

𝑥=2 e 𝑥=−2

Soluzione di Livello 2

Le soluzioni per questa equazione quadratica sono:

𝑥=2 e 𝑥=−2

Hai trovato entrambe le soluzioni? Ottimo lavoro! Questo ti prepara per sfide ancora più grandi.

CLICCA QUI E PASSA AL LIVELLO SUCCESSIVO

LIVELLO 1

Prendi carta e penna: Senza calcolatrice risolvi questa equazione di secondo grado in 60 secondi e dimostra le tue capacità

Sfida per aspiranti geni: Solo il 20% delle persone riesce a trovare la soluzione a questo test, e tu ci riesci?

Sfida a Livelli: Quasi nessuno supera questo livello, risolvi l’equazione e dimostra di essere un genio

Sfida a livelli: Continua la scalata per essere un genio, risolvi l’equazione del secondo livello e mostra le tue abilità

Sfida a livelli: La scalata per essere un genio, Risolvi l’equazione e passa al livello successivo per completare la sfida

A proposito dell'autore

RedazioneA